西三数学サークル通信(特別版)33号

　　　　　　西三数学サークル202３．11.10例会報告
★日時　１１月1０日（金）19時～21時　安城文化センター
★参加者　６名（発表　４人）　　亀井、榊原、山田、原田、鈴木康、広田
★レポート一覧
　１．「組合せ」　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(亀井)
　２．「球を使った∑ｋ2のモデルから考えるいろいろな問題」のアイデア　　（広田）　
　３．3次関数の問題　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（山田）
　４．三角比（図形と計量）に関するあれこれ
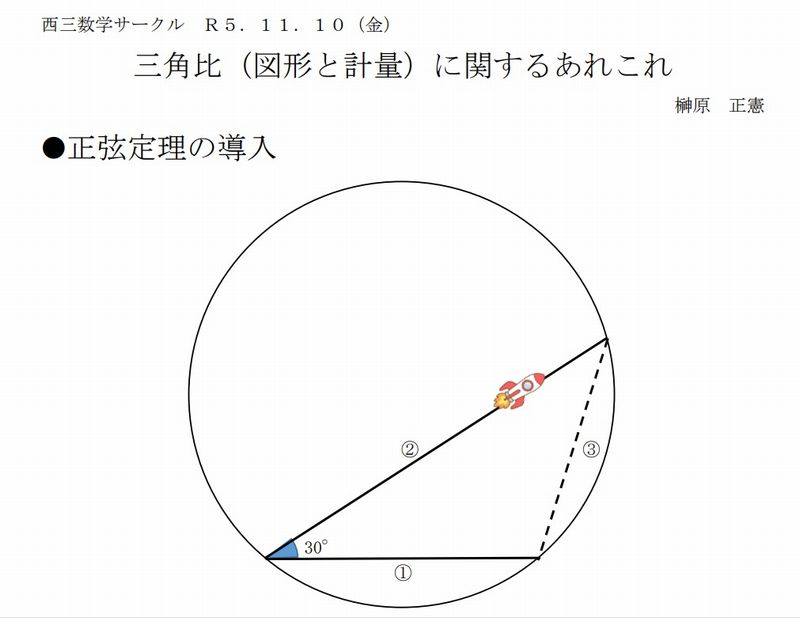
　　１）正弦定理の導入
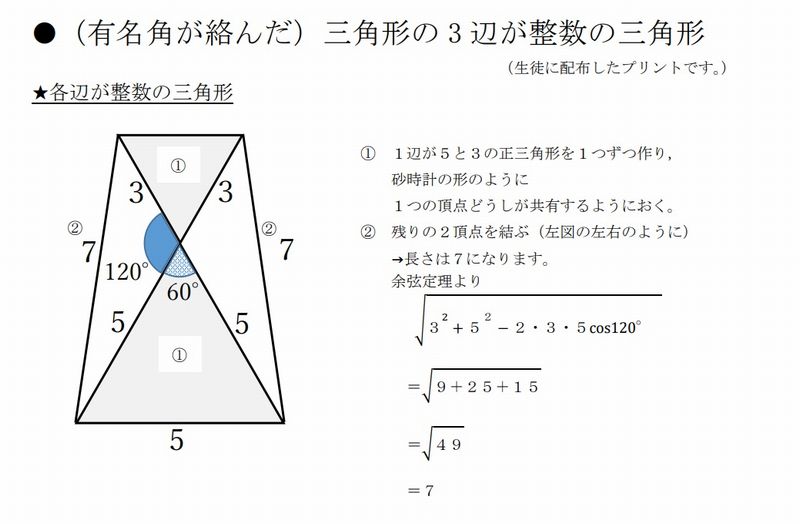
　　２）（有名角が絡んだ）三角形の3辺が整数の三角形　　　　　　　　　　　（榊原）　　

＊今回は遠路（岐阜）亀井さんが参加　恒例の近況報告からスタート。学校ではコロナだけでなく、
今はインフルエンザが流行っているらしい。サークルメンバーも高齢者が増えている。気を付けま
しょう。
＊１．は小学校でも組合せの考え方が登場している。高校までを見通して、言葉の定義だけではな
く「多元構造図」のグラフを使って考えてみようという問題提起。例えば、4個（以上）の集合の
ベン図が描けるかというような場面では有効と紹介。

＊２．は∑ｋ2　の球のモデルに発泡スチロール　を利用したもの。ビー玉では重く教室で見せるの
も大変だが、発泡スチロールなら10段モデルで385個、コストも1500円弱。接着は木工ボンドで、
色塗りもOK。モデルを見て、いろいろな問題を発展して考えてほしいと提起。

＊３．は3次関数のグラフを提示して関数の数式を選ぶ問題。従来の関数を与えてグラフ描きばか
りやる微分ではいやになるが、逆転の発想で道具としての微分でこうしてグラフ＝現象を調べられ
れば役に立つ数学の例として示すことができそうである。

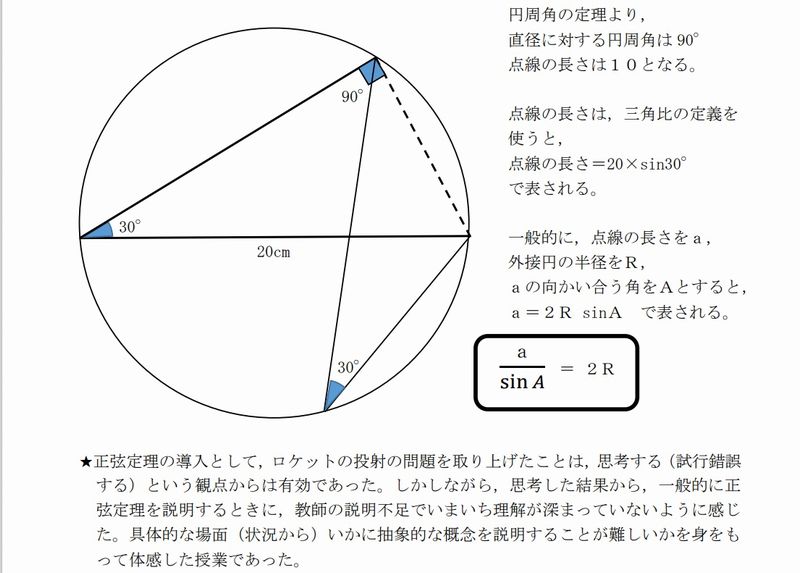
＊４．は１）正弦定理は定理を示して即証明ではなく、導入についていろいろ試みがあるが、円の
内部でロケットを投射して元に戻す問題で発射角と軌道の長さを考える問題。生徒の議論を作るこ
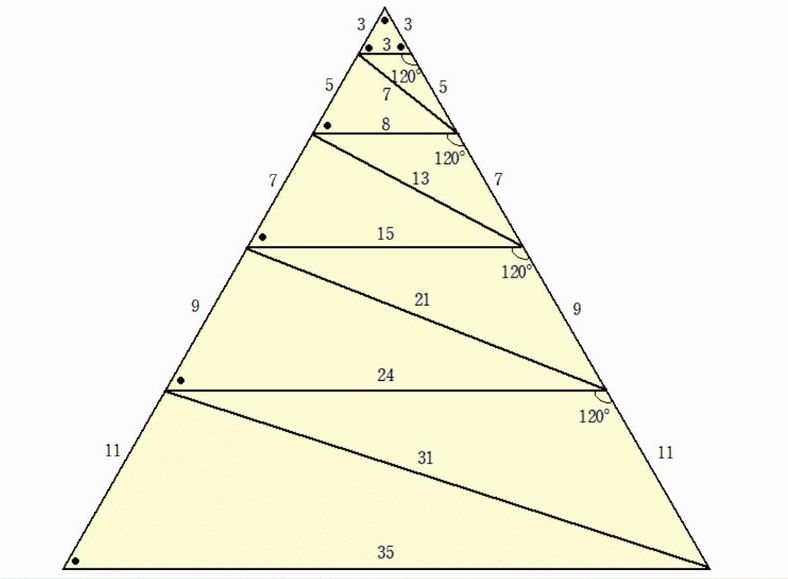
とができそうだ。２）は余弦定理でルートが外れて整数値が得られる（３辺が整数値の）貴重な（
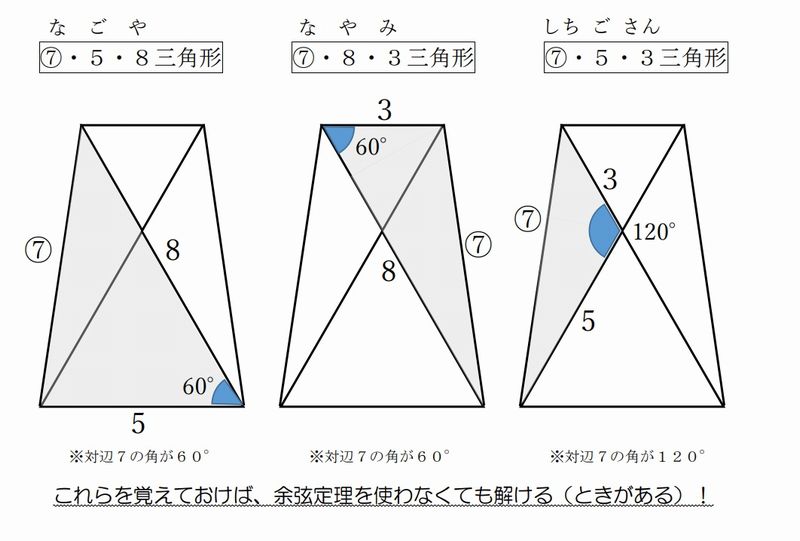
角度も得難い）三角形の紹介。手続を踏めば連続的なステップ（７・５・８）、（７・８・３）
（７・５・３）など得られる。
　＊１）は「生き生き数学」（三省堂　1987　何森仁他3名共著）にも別の導入例がある
　＊２）は「高校数学きれいに解ける問題つくり」（黎明書房　1988　斎木清治）でも紹介